Correlation is not causation!

Book of the month - September 2023 - Article 3

A fundamental principle in statistics and scientific research - "Correlation is not causation". But we still attribute of something which happens simultaneously as a potential cause. What it implies is that if two variables have a correlation with each other, it does not necessarily mean that one variable is causing the other to occur. In the book author mentions, an example of how between 1983-93 the butter production in Bangladesh is directly corelated to S&P 500 returns. They are corelated, but one is not causing another. If you look closely all controversial theories will fall into this category, that there is something which always is corelated but not necessarily causing it.  

Special thanks for the image and read more on: https://www.simplypsychology.org/correlation.html

This is because our brains are wired to look for causes and explanations everywhere even where they don’t exist. As humans we seek patterns that help us to predict the future and mitigate uncertainty. Our brains always working to develop explanations and attribute causes to events.

Here's a more detailed explanation:

Correlation: Correlation is a statistical measure that quantifies the degree to which two variables are related to each other. It can be positive (both variables increase together), negative (one variable increases as the other decreases), or zero (no apparent relationship). Correlation is often measured using coefficients like the Pearson correlation coefficient (for linear relationships) or the Spearman rank correlation coefficient (for non-linear relationships).

Causation: Causation, on the other hand, implies that one variable is causing the other to happen. In other words, a change in one variable directly leads to a change in the other. Establishing causation typically requires more than just observing a correlation. It often involves conducting controlled experiments, considering the temporal sequence of events, ruling out alternative explanations, and demonstrating a plausible mechanism by which one variable influences the other.

The phrase "correlation is not causation" serves as a reminder that just because two things happen together or seem related does not mean that one is causing the other. There may be confounding variables, coincidence, or other factors at play that create the observed correlation.

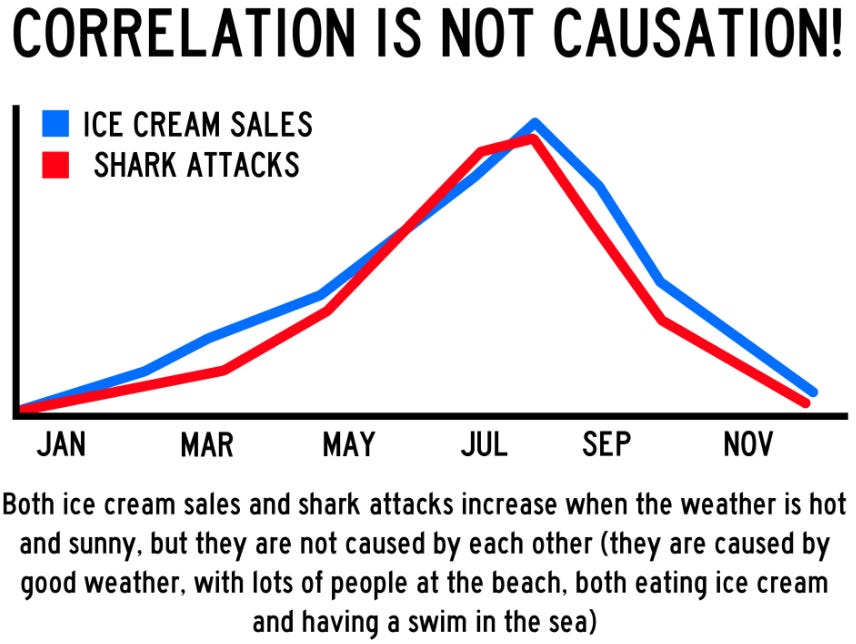
For example, imagine you observe a strong positive correlation between ice cream sales and drowning incidents during the summer months. It would be incorrect to conclude that buying ice cream causes people to drown. In reality, both of these variables are influenced by a common factor, which is hot weather. During the summer, people are more likely to buy ice cream because it's hot, and they are also more likely to swim, increasing the risk of drowning. Hot weather is the confounding variable in this case.

In scientific research and critical thinking, it's essential to go beyond correlations and establish causation through rigorous analysis and experimentation when necessary. This principle helps prevent making erroneous conclusions or taking inappropriate actions based solely on observed associations between variables.